A classic article by computer scientist Allen Downey on why there is only one statistical test: compute a test statistic from your observed data, simulate a null hypothesis, and finally compute/approximate a p-value by calculating the fraction of test statistics from the simulated data exceeding the test statistic from your observed data.
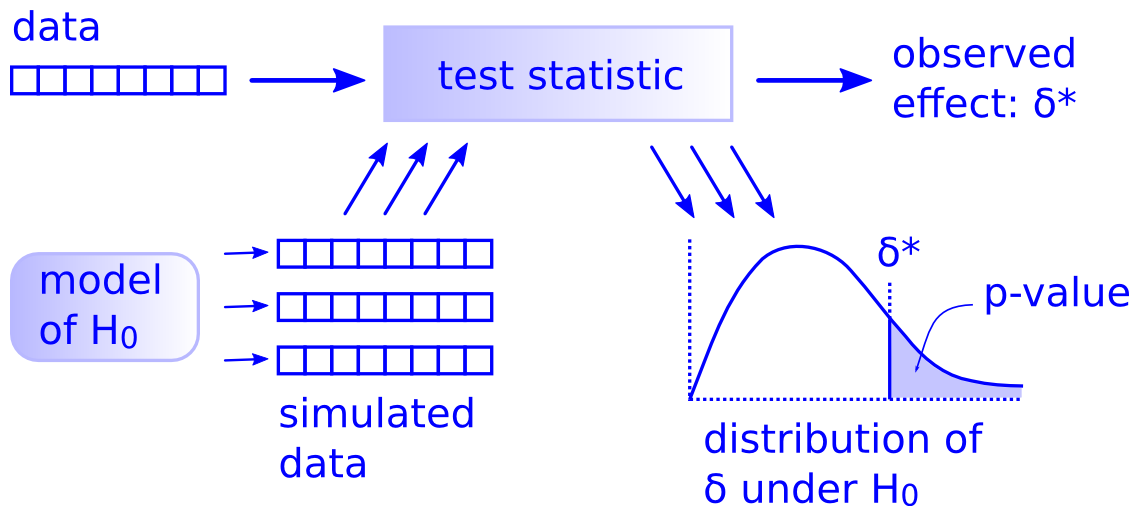
Downey suggests using general simulation methods over the canon of rigid, inflexible tests invented when computation was difficult and expensive.
Hat tip to Ryan Briggs on Twitter.